引入“动量项+自适应学习率”来进行BP算法改进,采用iris数据集进行了改进前后对比实验。
相关答案和源代码托管在我的Github上:PnYuan/Machine-Learning_ZhouZhihua.
问题回顾
解题过程
注:本题程序基于Python实现(这里查看完整代码和数据集)。
方法设计
传统的BP算法改进主要有两类:
- 启发式算法:如附加动量法,自适应算法。
- 数值优化算法:如共轭梯度法、牛顿迭代法、Levenberg-Marquardt法。
这里我们首先采用附加动量实现基本的方法改进。然后分析算法的不足,设计面向学习率的自适应机制来改进,实现基于动态自适应学习速率的BP算法改进。
附加动量项
这是一种广泛用于加速梯度下降法收敛的优化方法,其核心思想是:在梯度下降搜索时,若当前梯度下降与之前梯度下降方向相同,则加速搜索,反之则减速搜索。
参考书p103(式5.11),标准BP算法的参数更新项为:
∆ω(t) = ηg(t)
式中,∆ω(t)为第t次迭代的参数调整量,η为学习率,g(t)为第t次迭代所计算出的梯度。
在添加动量项之后,基于梯度下降的参数更新项为:
∆ω(t) = η[(1-μ)g(t)+μg(t-1)]
始终,μ为动量因子(取值0~1)。上式也等效于:
∆ω(t) = α∆ω(t-1)+ηg(t)
式中α被称为遗忘因子,α∆ω(t-1)代表之前梯度下降的方向和大小信息对当前梯度下降的调整作用。
自适应学习率
附加动量法面临学习率的选取的困难,进而产生收敛速度与收敛性之间的矛盾。于是另考虑引入学习速率自适应设计,这里给出一种自适应方案:
η(t) = σ(t)η(t-1)
上式中,σ(t)为第t次迭代时的自适应学习速率因子,下面是其一种计算实例:
σ(t) = 2^λ
其中λ为梯度方向:λ = sign(g(t)(t-1))
这样,学习率的变化可反映前面附加动量项中所说的“核心思想”。
算法总结
将上述两种方法结合起来,形成动态自适应学习率的BP改进算法:
学习算法原型可参照书p104算法图5.8,如下图所示:

从上图及书中内容可知,输出层与隐层的梯度项不同,故而对应不同的学习率 η_1 和 η_2,算法的修改主要是第7行关于参数更新的内容:
将附加动量项与学习率自适应计算代入,得出公式(5.11-5.14)的调整如下图所示:
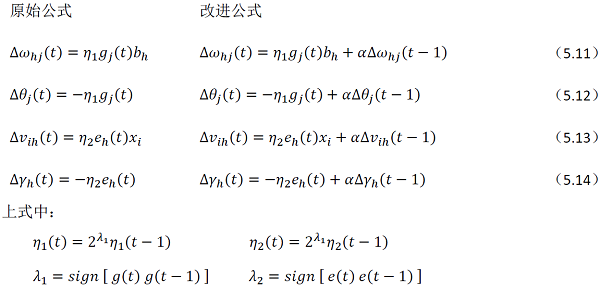
对比实验
(点击查看完整程序)
这里我们采用IRIS data set,实验基于python-pybrain实现,步骤如下:
1. 搭建网络:搭建单隐层网络;
2. 训练网络:分别采用学习率固定方案和动态调整方案来实现基于BP算法的模型训练;
3. 结果比较:比较训练过程中的参数或误差收敛情况以及最终的模型预测结果;
BP算法实现代码可参考神经网络基础 - 编程实现标准BP算法
数据预分析
iris(鸢尾花)数据集的一些基本信息如下(参考iris.names):
属性信息,4-输入(连续值),1-输出(标称值,3类):
Attribute Information:
1. sepal length in cm
2. sepal width in cm
3. petal length in cm
4. petal width in cm
5. class:
-- Iris Setosa
-- Iris Versicolour
-- Iris Virginica
样本规模(150条,均匀分3类):
Number of Instances: 150 (50 in each of three classes)
有无缺失值(无):
Missing Attribute Values: None
...
经过相关预检,可以看出该数据集规整度很高。
对其中的一些变量进行可视化如下图,可以看出其类别分散特性:
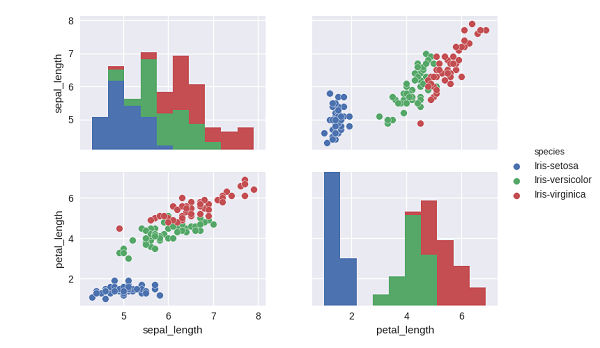
为了方便进行数值计算,采用独热编码(onehot encoding)对输出的标称数据进行数值化,这样输出由1维变为3维(每一个输出对应一类)。在最终结果处理时,可采用胜者通吃(winner-take-all)的准则选择数值最大的输出对应的类作为分类结果。
BP网络搭建
这里搭建单隐层前馈模型,三层节点数从输入到输出依次为 <4, n_h, 3>,其中隐层节点数 n_h 根据实验具体进展灵活取值。
下面是BP网络搭建样例代码:
1 | from BP_network import * |
固定学习率下的模型训练
为了研究学习率对模型训练的影响,这里分别设置三个学习率:很大、很小和合适,分别得出对应训练误差曲线如下图所示:
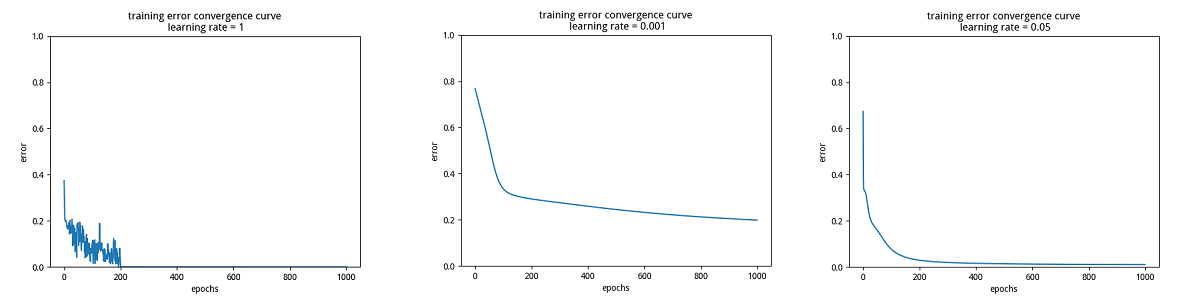
分析上面的图,可以看出,当学习率过大时,收敛过程出现了严重的振荡,当学习率过小时,收敛过慢,当采用合适的学习率时,收敛过程稳定。
自适应学习率下的模型训练
根据上面关于学习率过大过小的对比实验,这里先为学习率的调整设置上下限。然后实现动态学习率下的标准BP算法。
最后得出固定学习率与动态学习率下训练误差收敛曲线对比如下图:
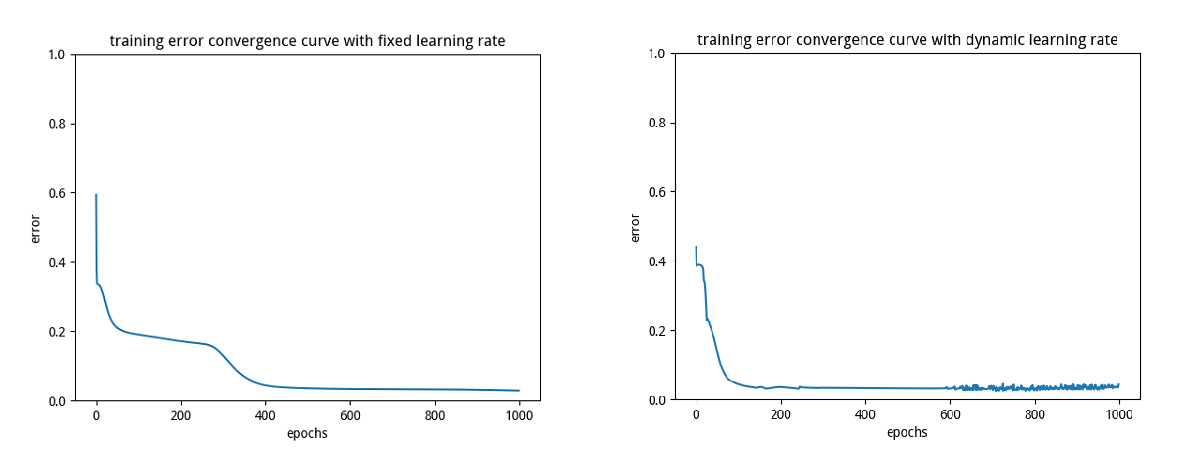
可以看出,动态学习率的收敛速度较快,两种机制在足够多的迭代步骤后均实现了良好的精度。(另外我们看到,动态调整学习率下的收敛曲线最后阶段发生了轻微振荡,这和学习率的调整幅度(底数及遗忘系数有关系。这两个参数需要人工调试)有关)。
下面是最终的测试集预测误差结果:
固定学习率:test error rate: 0.013
动态学习率:test error rate: 0.027
本题小结
采用动态调整学习率的确能够大幅提升BP算法的收敛速度,在数据量很大时愈发明显。但同时也要注意学习率的取值区间和相关加速参数的设置,以期实现最优性能。
